Scaling Shapes Lesson Plan: PhET Interactive Simulations
Submitted by: Amanda McGarry, PhET Interactive Simulations
In this lesson plan, students use an interactive simulation to predict the area and perimeter of shapes that have been scaled by factors of 2 or 3. Then they’ll generalize how the area and perimeter of a shape will change after being scaled by a factor of s.
Students will:
- Predict the area and perimeter of shapes that have been scaled by factors of 2 and 3.
- Generalize how the area and perimeter of a shape will change after being scaled by a factor of s.
Materials:
- Computers or other devices with Internet access
- Scaling Shapes Activity Sheet
- Pink and blue sticky notes
Preparation:
This lesson features an interactive simulation titled Area Builder, developed by our award-winning partner PhET through the University of Colorado Boulder. The simulation challenges students to build shapes and explore the relationship between area and perimeter through two types of challenges: “Build a Shape” and “Find the Area.” Each type of challenge includes increasing levels of difficulty.Photocopy a class set of the Scaling Shapes activity page.
Watch the Area Builder video primer for an introduction to the Area Builder simulation’s features and uses. Then watch the Area Builder Simulation Overview for a summary of the of sim controls, model simplifications, and insights into student thinking.
Preview and play with the Area Builder simulation to plan how you will adapt it to your students’ needs. If students will be working in small groups, review tips on Setting Cooperative Gaming Expectations.
Depending on your classroom routines and available technology, you may want to consider these grouping options:
- 1:1 with students and devices
- Two to three students sharing one device and swapping ideas and the device back and forth
- Station model where small groups rotate through using the devices.
Build background knowledge or reinforce topics with these BrainPOP movies: Area of Polygons, and Geometry. BrainPOP Jr also offers a movie about Area.
Lesson Procedure:
- Activate Prior Knowledge. Activate prior knowledge by having students journal about the following prompt (you can ask this about each set of figures):
Are these two figures similar? Explain how you know. Find the scale factor, if applicable.
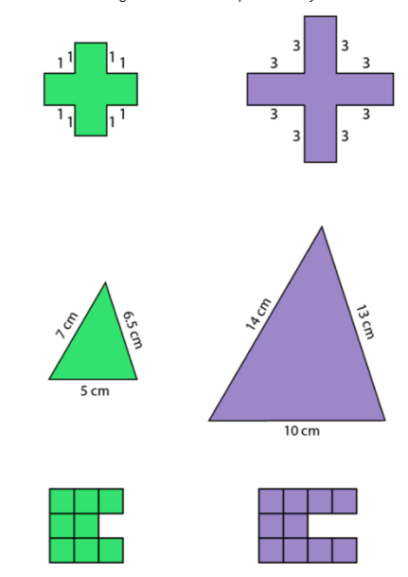
- Have students discuss their responses with a partner. Then have them share their responses with the class.
- Introduction
-
- Model for the class on a whiteboard how to access the Area Builder sim. Then working independently or with a partner, have students play with the Explore screen for 5 minutes before starting the activity.
- Ask students to share any tools they uncovered that you think would be useful for the activity, such as the dimensions tool.
-
- Then distribute the activity Scaling Shapes Activity Sheet to each student to work work individually or with a partner, discussing prompts on the activity sheet.
-
- Guided Exploration Students use the Area Builder sim to complete the Scaling Shapes Activity Sheet. They build a shape on their own, and then trade computers with a partner. Next, they make predictions and test by building a scaled shape. Finally, they compare results.
- Circulate as students are working and ask the following prompts if needed:
- How did you come up with your prediction?
- Why is #2 limiting the side length to 4 units?
- Are you surprised at the results for area and perimeter of your scaled shape? What do you think the rule is?
- What patterns do you notice?
- How did you come up with your prediction?
- How will you build your scaled shape? What is your strategy?
- In small groups, have students discuss Part III of the Scaling Shapes Activity Sheet and write observations about perimeter on the pink sticky notes and area on blue sticky notes. When they are done, have them place their sticky notes on the t-chart.
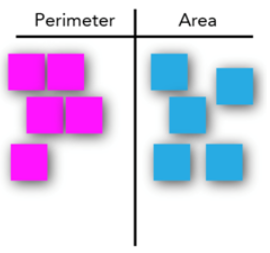
- Discuss
Prompt a class discussion about students’ experience using a teaching strategy such as popcorn discussion (one student answers, calls on the next student to talk), think-pair-share (pose question, allow time to think, turn and talk to partner), or group discussions (print out questions and have groups talk to each other and write down consensus to share aloud with class). Sample questions include:
- What is the rule for calculating the new perimeter of a scaled shape? How do you know?
- What is the rule for calculating the new area of a scaled shape? How do you know?
- Why are the rules different for perimeter and area?